Covering the Space of Tilts
Full Title: “Covering the Space of Tilts: Application to affine invariant image comparison”
Authors: Mariano Rodríguez, Julie Delon and Jean-Michel Morel
Journal: SIIMS
Abstract: We propose a mathematical method to analyze the numerous algorithms performing Image Matching by Affine Simulation (IMAS). To become affine invariant they apply a discrete set of affine transforms to the images, previous to the comparison of all images by a Scale Invariant Image Matching (SIIM), like SIFT . Obviously this multiplication of images to be compared increases the image matching complexity. Three questions arise: a) what is the best set of affine transforms to apply to each image to gain full practical affine invariance? b) what is the lowest attainable complexity for the resulting method? c) how to choose the underlying SIIM method? We provide an explicit answer and a mathematical proof of quasi-optimality of the solution to the first question. As an answer to b) we find that the near-optimal complexity ratio between full affine matching and scale invariant matching is more than halved, compared to the current IMAS methods. This means that the number of key points necessary for affine matching can be halved, and that the matching complexity is divided by four for exactly the same performance. This also means that an affine invariant set of descriptors can be associated with any image. The price to pay for full affine invariance is that the cardinality of this set is around 6.4 times larger than for a SIIM.
Visualising non optimal and near optimal coverings
This section explains who to quickly load coverings of the Space of Tilts: found in the literature; or those from our work, i.e. near optimal ones. All those coverings can be visualised in MATLAB with our Tester source code.
Modify (if needed) and execute the script “scripts/coverings2file_auto.m” to visually generate coverings in 2D and 3D. Those visualising functions are very demanding in terms of memory (Sorry about that !). You might want to disable 3D visualisation by modifying the script.
The reader will also notice that the variables covering and filename in the script are used to control which coverings will be printed from “get_feasible_covering.m” and “get_literature_covering.m”.
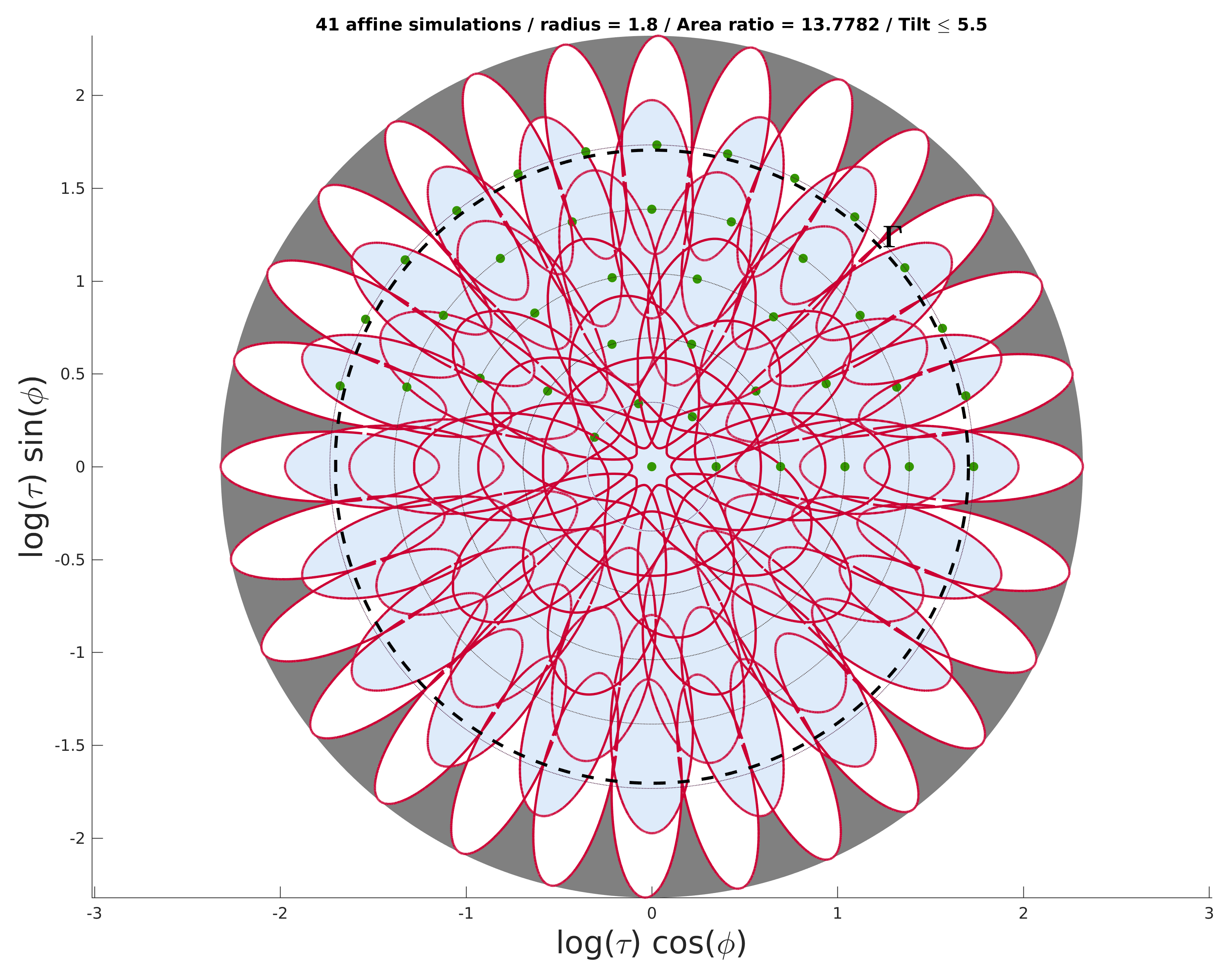
Or you can just display a single covering with the following code:
[ tvec, psicell, radius, region ] = get_literature_covering('ASIFT');
val = 0; count =0;
for i=1:length(tvec)
t=tvec(i);
numphi=length(psicell{i});
count = count + numphi;
val = val + numphi/t;
end
% 2D drawing
optionsdraw.tilt = [region];
optionsdraw.draw_regions = true;
optionsdraw.draw_regions_tilt = max(tvec(:))*radius;
draw_ball_pol(tvec,psicell,log(((radius))),optionsdraw);
htitle = get(gca,'Title');
title( [get(htitle,'String') ' / radius = ' num2str(radius) ' / Area ratio = ' num2str(val) ' / Tilt \leq ' num2str(region)]);
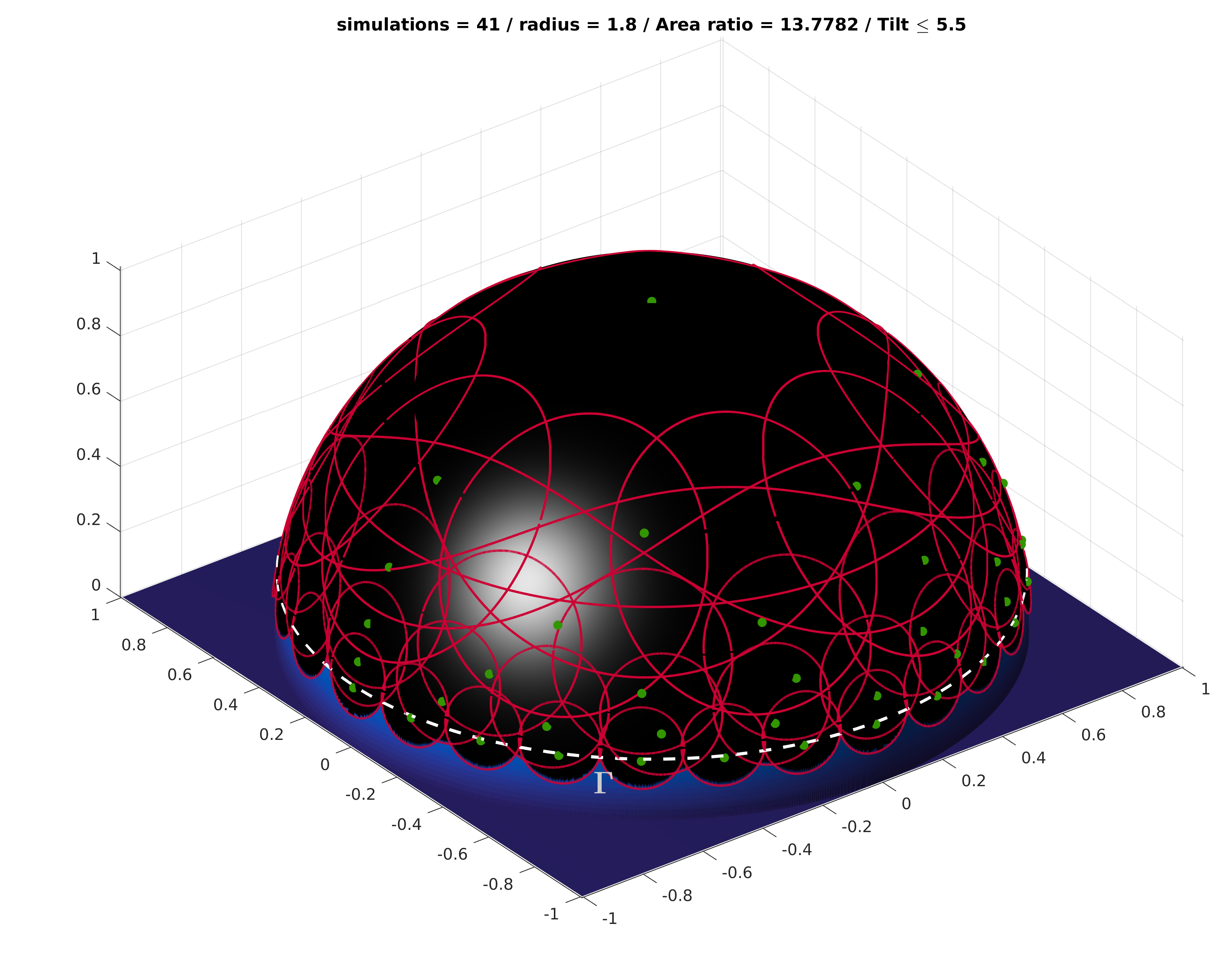
% 3D drawing
optionsdraw.tilt = [region];
draw_ball3d(tvec,psicell,log(radius),optionsdraw);
title( ['simulations = ' num2str(count) ' / radius = ' num2str(radius) ' / Area ratio = ' num2str(val) ' / Tilt \leq ' num2str(region)]);
which would display the following
Estimating transition tilt tolerances
In order to estimate the transition tilt tolerance of a SIIM-Matcher,a set of MATLAB functions in our Tester source code may be used.
The tester already comes with the image data base proposed in this paper. They are called upon by “tolerance_tests_SIIMS.m” which in fact calls all images inside the folder image_BD. Feel free to modify this folder if you want to change the image data set. These series of test will also run the function “perform_tilt_on_image.m” which is in fact a C++ function that will be automatically compiled with MEX (the matlab c++ compiler).
(Optional) Preparing an external tester
Put the SIIM-Matcher you would like to test inside the folder siim-matcher and under the name main. In order to well handle your SIIM-Matcher, please modify the % EXECUTION OF THE SIIM-MATCHER part inside the file “tolerance_tests_SIIMS.m”. The idea is to run your matcher follow by an Homography filter (like USAC Homography or ORSA Homography) for the pair of matlab generated images
and return the number of matches to the variable num_matches.
Executing the tester in MATLAB
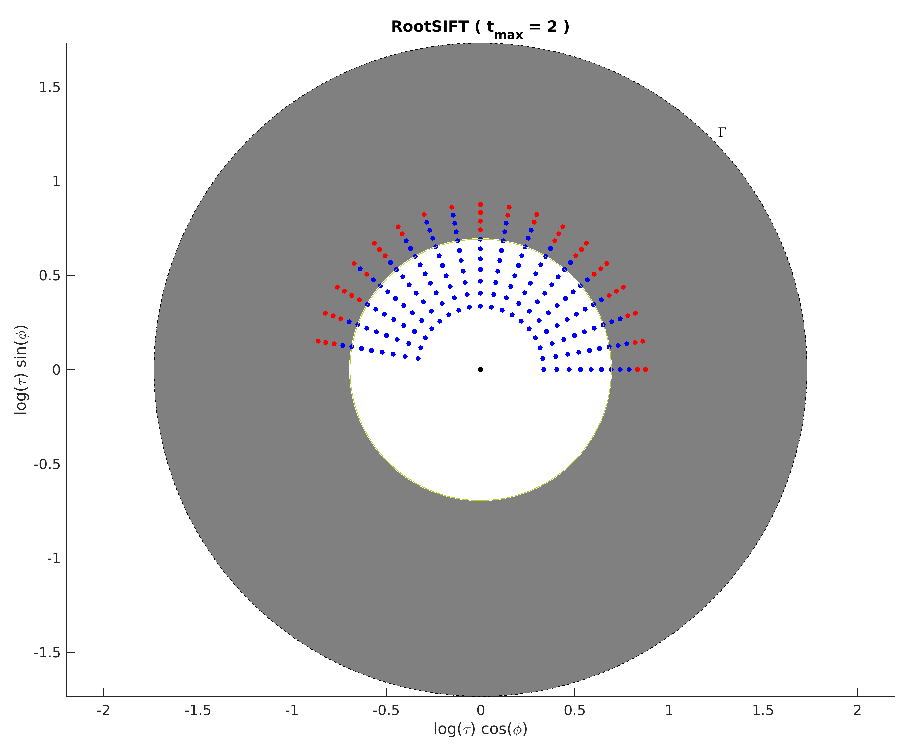
The figures and test in this paper were obtained by executing the following code for each of the SIIM-Matchers (SIFT, RootSIFT, SURF, FREAK, AKAZE, BRISK, ORB, BRIEF, LATCH).
opts_maxtilt.draw_on = true;
anglevec = 0:10:170;
tvec = 1.2:0.1:2.4;
figure;
[Mbool, Mval, RADIUS ] = tolerance_tests_SIIMS(tvec,anglevec,opts_maxtilt);
title(['Transition Tilt Tolerance t_{max} = ' num2str(RADIUS) ' )']);
For example, the above code run together with a RootSIFT Matcher would output a maximal tilt tolerance t=2 and reproduce the following figure: